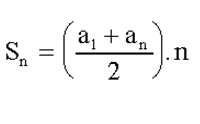Exercícios - Progressão Aritmética (PA) - Progressão Geométrica (PG)

                      P.A  e  P.G - Lista de Exercícios – Ensino Médio - 1° série A – B - C

Progressão Aritmética:

Fórmula do termo Geral da P.A.

a_n = a₁ + (n-1).r

Soma dos Termos da P.A.

Progressão Geométrica (P.G):

Fórmula do Termo Geral da P.G.

a_n = a₁ . q^n-1

Soma dos Termos da P.G.

P.G. limitada (ou finita):

                                                           Exercícios

1) Uma empresa deve instalar telefones de emergência a cada 42 quilômetros, ao longo da rodovia de 2.184 km, que liga Maceió ao Rio de Janeiro. Considere que o primeiro desses telefones é instalado no quilômetro 42 e o último, no quilômetro 2.142. Assim, a quantidade de telefones instalados é igual a:

a) 50            b) 51             c) 52                d) 53

2) Inserindo-se 5 números entre 18 e 96, de modo que a sequência (18, a₂, a₃, a₄,a₅,a₆, 96) seja uma progressão aritmética, tem-se a₃ igual a:

a) 43         b) 44          c) 45       d) 46       e) 47

3) Um pai resolve depositar todos os meses uma certa quantia na caderneta de poupança de sua filha. Pretende começar com R$ 5,00 e aumentar R$ 5,00 por mês, ou seja, depositar R$ 10,00 no segundo mês, R$ 15,00 no terceiro mês e assim por diante. Após efetuar o décimo quinto depósito, a quantia total depositada por ele será de:

a) R$ 150,00       b) R$ 250,00        c) R$ 400,00        d) R$ 520,00      e) R$ 600,00

4) Dada a progressão geométrica 1, 3, 9, 27, ..... se a sua soma é 3280, então ela apresenta:

a) 9 termos         b) 8 termos         c) 7 termos          d) 6 termos         e) 5 termos

  

5) Num programa de condicionamento físico uma pessoa começa correndo 300 metros num dia, 400 metros no dia seguinte, 500metros no próximo dia e assim sucessivamente até o décimo dia.Pergunta-se:

a)Quantos  metros correu no décimo dia?

b)Qual o total de metros percorridos por essa pessoas nos 10 dias?

6) Calcule o valor de x para que os números (2x; 1-7x; 3x-11) nesta ordem, formem uma P.A.

7)Para que valor de x a sequência (x-4; 2x; x+2) é uma P.A?

 8) Calcule a soma dos 25 primeiros termos da P.A(1;3;5;...)

 9) Se o preço de um carro novo é R$ 20.000,00 e esse valor diminui R$ 1200,00 a  cada ano de uso, qual será o preço deste carro após 5 anos de uso?

 10) Interpole 6 meios aritméticos entre 100 e 184.

11) Calcule o 1° termo da P.G em que  a₄=64 e q=2.

12) Qual é a razão de uma P.G em que a₁= 4 e  a₄= 4000?

13) Numa P.G, temos a₅=32 e a₈=256.Calcule o primeiro termo e a razão dessa P.G.

Gabarito

1 - Alternativa  B

2 - Alternativa  B

3 - Alternativa E

4 - Alternativa B

5.a - Resp: 1200m

5.b - Resp: 7500m

6 - X=13/19

7 - X=-1

8 - Resp: S₂₅=625

9 - Resp: R$14.000,00

10 - Resp: ( 100, 112, 124, 136, 148, 160, 172, 184)

11 - Resp: a₁=8

12 - Resp: q=10

13 - Resp: a₁=2 e q=2.

Logaritmos - Exercícios resolvidos

EXERCÍCIOS RESOLVIDOS - LOGARÍTMOS

1) Construa o gráfico das funções.

Solução. Atribuindo alguns valores para x > 0 em (a) e x > 1 em (b), temos:

a) f(x) = log₃ x

b) f(x) = log₂ (x – 1)

OBSERVAÇÕES:

1)     O 1º gráfico NÃO intercepta o eixo Y. Isto é, não há valores de “x” tal que f(x) = 0.

2)     O 2º gráfico NÃO intercepta o eixo Y. Mais que isso! A condição (x – 1) > 0 indica que a curva margeia a reta vertical x = 1, sem tocá-la.

2) Resolva as equações.

Solução. Depois de encontradas as soluções devem obedecer às condições de existência dos logaritmos. (log_aN existe se: 0 < a ≠ 1 e N > 0).

a) log₂ (2x – 5) = log₂3   

       

b) log₃ (3 – x) = log₃ (3x + 7)           

       

 c) log₅ (2x – 3) = 2

d) log₂ (x² + x – 4) = 3        

                                                     

e     e) 2.log x = log (2x – 3) + log (x + 2)      

                       

     f) log₄ x + log_x 4 = 2       

                 

3)   Coloque V (verdadeiro) ou F (falso) nas sentenças.

     

  Solução. Para resolver essas questões é necessário lembrar.

a)     Se a > 1, então a função logarítmica f(x) = log_ax é crescente: x₁ < x₂ então f(x₁) < f(x₂).

b)     Se 0 < a < 1, então a função logarítmica f(x) = log_ax é decrescente: x₁ < x₂ 

então os valores  são f(x₁) > f(x₂).

4) 4)

4)  O pH de uma solução é o logaritmo decimal do inverso da concentração de H₃O⁺.

 Qual o pH de uma solução cuja concentração de H₃O⁺ é 4,5.10^-5 mol /l ?

Solução. Substituindo os valores indicados, temos:

5) Calcule a meia-vida de uma substância radioativa que se desintegra a uma 

taxa de 4% ao ano.

 (Meia-vida é o tempo que deve decorrer para que, em certo momento, 

metade dos átomos de uma substância radioativa se desintegre.)

Solução. 

A expressão para a situação descrita pode ser representada por: Q(t) = Q₀.e^{- rt}.

6) Uma pessoa coloca R$ 1000,00 num fundo de aplicação que rende, em média, 1,5% a.m. 

Em quantos meses essa pessoa terá no mínimo R$ 1300,00? (Use a calculadora)

Solução. Utilizando a teoria de matemática financeira, temos:

7) A intensidade I de um terremoto, medida na escala Richter,

 é um número que possui variação entre I = 0 até I = 8,9 para maior  terremoto conhecido.

 I é dado pela fórmula: 

na qual E é a energia liberada no terremoto em quilowatt-hora e E₀ = 7.10^-3 kwh.

a)     Qual a energia liberada num terremoto de intensidade 8 na escala Richter?

Solução. Substituindo os valores, temos:

b)     Aumentando de uma unidade a intensidade do terremoto, por quanto fica multiplicada a

 energia liberada?

Solução. Substituindo os valores com I = 9, temos:

8) São necessários 5 anos para que o cobalto-60 perca a metade de sua radioatividade. 

Qual é a porcentagem de sua atividade original que permanecerá no fim de 20 anos?

Solução. 

A função será:

 Repare que N(5) = N₀/2. Ao longo de 20 anos, temos:

“Se deres um peixe a um homem faminto, vais alimentá-lo por um dia. 

Se o ensinares a pescar, vai alimentá-lo toda a vida.”

Lao-Tsé