Volume de Sólidos Geométricos
Professor Leoni Rodrigues Dantas
Dizemos
que o volume de um corpo é o espaço que ele ocupa. Esses corpos possuem
capacidade de acordo com o tamanho de suas dimensões. Observe as principais
medidas de volume e sua correspondência com a capacidade:
1m³ (metro cúbico) = 1 000 litros
1dm³ (decímetro cúbico) = 1 litro
1cm³ (centímetro cúbico) = 1 mililitro
Para determinarmos o volume de um corpo precisamos multiplicar a área da base e a altura. Lembrando que a base de uma figura pode assumir variadas dimensões (triângulos, quadriláteros, pentágonos, hexágonos, heptágonos entre outros). Alguns sólidos recebem nomes e possuem fórmula definida para o cálculo do volume.
1m³ (metro cúbico) = 1 000 litros
1dm³ (decímetro cúbico) = 1 litro
1cm³ (centímetro cúbico) = 1 mililitro
Para determinarmos o volume de um corpo precisamos multiplicar a área da base e a altura. Lembrando que a base de uma figura pode assumir variadas dimensões (triângulos, quadriláteros, pentágonos, hexágonos, heptágonos entre outros). Alguns sólidos recebem nomes e possuem fórmula definida para o cálculo do volume.
Prisma
Os prismas são sólidos em que o volume depende do formato da base. Para isso precisamos saber qual a fórmula indicada para calcular, primeiramente, a área da base de um prisma e, posteriormente, determinar o volume.
Paralelepípedo
Uma
piscina possui o formato de um paralelepípedo com as seguintes dimensões: 10
metros de comprimento, 6 metros de largura e 1,8 metros de profundidade.
Determine o volume e a capacidade da piscina.
V = a * b * c
V = 10 * 6 * 1,8
V = 108 m³ ou 108 000 litros
V = 10 * 6 * 1,8
V = 108 m³ ou 108 000 litros
Pirâmide
As pirâmides podem possuir em sua base um triângulo, um quadrilátero, um pentágono, um hexágono entre outros. A fórmula para determinar o volume de uma pirâmide é:
As pirâmides podem possuir em sua base um triângulo, um quadrilátero, um pentágono, um hexágono entre outros. A fórmula para determinar o volume de uma pirâmide é:
Exemplo:
Determine
o volume de uma pirâmide quadrangular medindo 6 metros de comprimento e altura
igual a 20 metros.
Cone
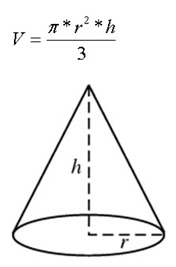
A base de um cone possui o formato circular. Para determinar o volume de um cone utilizamos a seguinte fórmula:
A base de um cone possui o formato circular. Para determinar o volume de um cone utilizamos a seguinte fórmula:
Exemplo:
Um
reservatório tem o formato de um cone circular reto invertido, com raio da base
medindo 5 metros e altura igual a 10 metros. Determine o volume do
reservatório.
Cilindro
O cilindro possui a base superior e base inferior no formato circular. Seu
volume é dado pela fórmula:
Exemplo:
Vamos calcular o volume de um cilindro circular com
raio da base medindo 8 cm e altura igual a
20 cm.
Esfera
A esfera é um corpo circular maciço, formado pala rotação de um semicírculo. O volume da esfera é dado pela expressão:
A esfera é um corpo circular maciço, formado pala rotação de um semicírculo. O volume da esfera é dado pela expressão:
Exemplo:
Determine
o volume da esfera que possui raio igual a 3 metros.











Nenhum comentário:
Postar um comentário